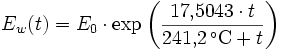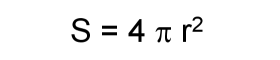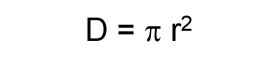> ACCENT de > Nr 7 März 2006 Klimamodellierung > C: Einfache Modelle
|
 |
Context: Einfache Modelle
|
|
Unsere Umwelt folgt physikalischen Gesetzen. Diese Gesetze werden in Gleichungen ausgedrückt. Freilich ist die Natur um uns herum sehr komplex. Es ist viel einfacher zu sagen, wie viel Energie benötigt wird, um einen Liter Wasser von 10°C auf 11°C zu erwärmen, als das Klimasystem in Gleichungen zu beschreiben. Wir können allerdings anhand einiger einfacher Gleichungen zeigen, wie dies prinzipiell funktioniert.
|
Wie können Klimafaktoren mit Hilfe einer Formel beschrieben werden?|
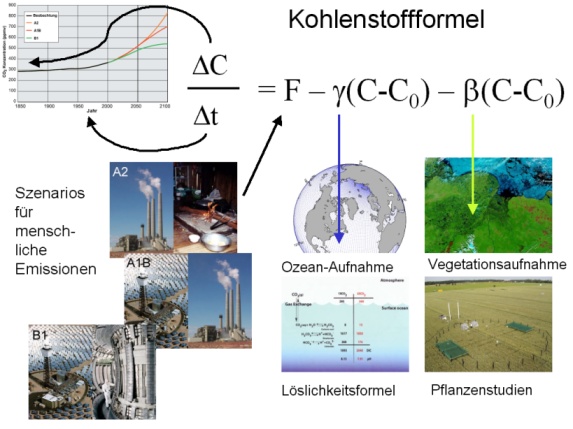
Seit dem Beginn der industriellen Revolution haben wir mehr und mehr sogenannte fossile Brennstoffe wie Kohle, Öl oder Erdgas verbraucht, um unsere Güter zu produzieren und unsere Häuser zu heizen. Ein Produkt des Verbrennungsprozesses ist das Treibhausgas Kohlendioxid (CO2). Oft wird in Tonnen Kohlenstoffatome C angegeben wie viel wir in die Atmosphäre entlassen haben. Allerdings verbleibt nicht jede als CO2 freigesetzte Tonne C für immer in der Luft. Pflanzen nehmen CO2 auf, um zu wachsen (manchmal mehr als sie freisetzen, wenn sie absterben) und eine Menge an CO2 wird in den Weltmeeren gelöst. Wir können dies in einer einfachen Gleichung für die Kohlenstoffbilanz ausdrücken.
|
 |
|
|
1. Kohlenstoffformel: Wie können wir zukünftige Änderungen von Kohlendioxid in der Luft vorhersagen?Der Gehalt an Kohlenstoff in der Luft (als Kohlendioxid) wird sich auch zukünftig mit den Jahren ändern. Klimamodelle beschreiben in einer Kurve, welche Änderungen wir für die nächsten Jahre erwarten können. Dies ist der linke Teil der Gleichung. Aber von welchen Faktoren hängt dies ab? Zunächst gibt es die vom Menschen verursachten Emissionen F. Für die Vergangenheit können wir in etwa sagen, wie viel CO2 wir ausgestoßen haben. Für die Zukunft müssen wir verschiedene Szenarien annehmen. Von der Gesamtmenge, die vom Menschen ausgestoßen wird, müssen wir den Anteil (beta) abziehen, der von den Pflanzen aufgenommen wird sowie den Anteil (gamma), den die Ozeane aufnehmen. Die Aufnahmekoeffizienten werden mit der Menge Kohlenstoff multipliziert, die wir der Atmosphäre zugeführt haben. Dies bedeutet die Differenz zwischen dem derzeitigen Kohlenstoffgehalt C und dem vorindustriellen Kohlenstoffgehalt C0. Wissenschaftler erhalten das Gamma aus einer Formel für die Löslichkeit und schätzen Beta anhand von Pflanzenuntersuchungen ab.
|
|
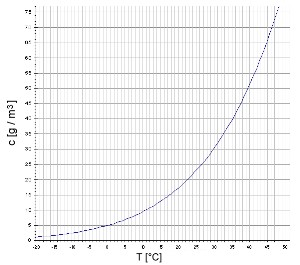
Klimamodelle prognostizieren, dass es im Durchschnitt in einer wärmeren Welt mehr und stärkeren Regen geben wird. Warum ist dies so? Warme Luft kann mehr Wasser halten als kalte. Dies zeigt die Sättigungskurve rechts. Die Gleichung für diese Kurve ist recht kompliziert.
|
Hinter der Kurve verbergen sich thermodynamische Ausdrücke wie die Clausius-Clapeyron Formel:
oder, vereinfacht, die Magnus Formel:
Es ist nicht notwendig, die Formeln herzuleiten. Wir sehen aber, dass es sich um eine exponentielle Beziehung handelt vom Typ: Der maximale Wasserdampfgehalt der Luft steigt also exponentiell mit der Temperatur. |
|
|
|
|
Steigt die durchschnittliche Energie nahe der Erdoberfläche, so verdunstet mehr Wasser und mehr Wasser fällt auch wieder zur Erde. Der Wasserkreislauf intensiviert sich. Dies bedeutet jedoch nicht unbedingt, dass auch mehr Regen über Land fällt. Das meiste Wasser verdunstet über den Ozeanen und es hängt von den Windsystemen ab, wo es wieder zur Erde fällt.
|
|
Wenngleich sich die durchschnittliche Temperatur auf der Welt über die letzten 50 Jahre erhöht hat, zeigen Niederschlagsmessungen, dass es für den mittleren Niederschlag über Land keinen klaren Trend gibt. Starke Vulkanausbrüche können den durchschnittlichen Niederschlag für mehr als ein Jahr senken. Anzeichen für einen Zusammenhang mit der Temperatur gibt es jedoch nicht. |
 |
|
|
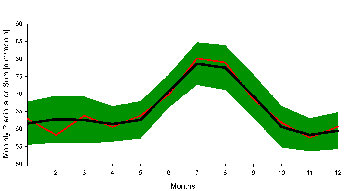
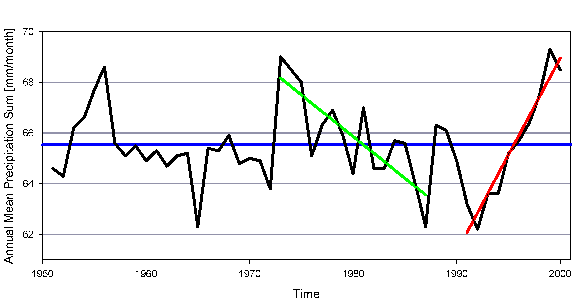
4. Zeitreihe für den mittleren monatlichen Niederschlag über der weltweiten Landfläche (Grönland und die Antarktis sind nicht eingeschlossen). Blaue Linie: Trendlinie für den gesamten Zeitraum 1951 bis 2000, grüne Linie: linearer Trend der Zeit von 1971 bis 1987, rote Linie: Trend für den Zeitraum 1991 bis 2000
|
|
Die untersuchte Landoberfläche macht (ohne Grönland und Antarktis) macht jedoch nur 25% der gesamten Erdoberfläche aus. Wir können daher erahnen, dass es nicht einfach ist vorherzusagen, in welcher Weise uns die Intensivierung des globalen Wasserkreislaufes in der Zukunft betreffen wird, wenngleich die Antwort aus der Sättigungskurve einfach erscheint: mehr Regen.
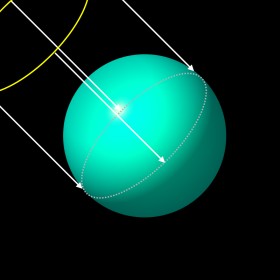
Die Energie, die unser Klimasystem antreibt und die Erde für das Leben auf ihr warm genug hält, kommt von der Sonne. Natürlich muss die Erde diese Energie auch wieder zurücksenden. Anderenfalls würde sie wärmer und wärmer. Können wir diesen Vorgang in Gleichungen ausdrücken? Die Sonne sendet ihre Energie in nahezu parallelen Strahlen zur Erde. Diesen Energiefluss bezeichnen wir als Sonnenkonstante L. Er wird in der Einheit Leistung pro Fläche angegeben und hat einen Wert von etwa 1366 W/m2. Gäbe es keine Reflexion, so würde ein Viertel dieser Energie unsere Atmosphäre treffen. Warum ist es ein Viertel? Es erreicht uns nur ein Viertel der Sonnenkonstante, da die volle Energie nicht überall senktrecht auf die Erde trifft. Wir wissen, dass auf einer Hälfte der Erdkugel immer Nacht ist und die Sonnenstrahlung unter einem niedrigeren Einfallswinkel schwächer ist. Da der Querschnitt einer Kugel ein Viertel ihrer Oberfläche ist, gilt für die Gesamtenergie, die auf die Erde trifft R = 1/4 L = 342 W/m2. |
|
|
|
|
|
|
|
Ein Teil der Sonnenstrahlung wird jedoch von der Erdoberfläche nicht aufgenommen (absorbiert), da sie reflektiert wird, z.B. durch Wolken, Eis und Schnee. Wir bezeichnen diesen Anteil als die Albedo A der Erde. Der reflektierte Anteil liegt im Bereich von 30% der einfallenden Sonnenstrahlung. Die einfallende Energie ist daher: |
 |
|
|
|
|
Die Temperatur der Erde würde stetig steigen, würde sie nicht die aufgenommene Energie wieder abgeben. Wir wissen aus dem Stephan-Boltzmann Gesetz (für Schwarzkörper-Strahlung), dass die Rate, mit der Infrarotstrahlung von einem warmen Körper abgestrahlt wird, als eine einfache Funktion der Temperatur errechnet werden kann: |
 |
|
|
|
|
Sigma ist die Stefan-Boltzmann Konstante und Te ist die Temperatur der Erdoberfläche. Folglich können wir das Strahlungsgleichgewicht durch das folgende Gleichungssystem beschreiben: |
 |
|
|
|
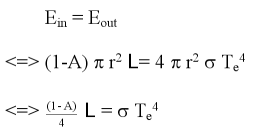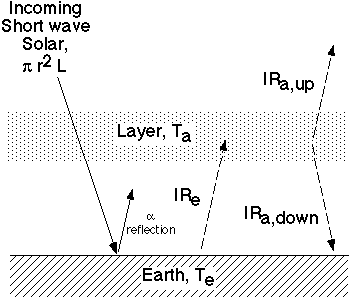
Dies ist die Grundgleichung der Energiebilanz der Erde ohne Einbeziehung der Treibhausgase. Beziehen wir die Treibhausgase mit ein, so wird ein Teil der abgestrahlten Infrarotenergie auf der rechten Seite der Gleichung wieder zur Erde zurückgesandt, wie es in der Abbildung rechts gezeigt ist. Gleichzeitig erhöht sich aber auch die Temperatur der Erdoberfläche. Die Gleichungen werden etwas komplexer. Wir können uns jedoch vorstellen, dass das System mathematisch zu beschreiben ist.
|
|
|
|
|
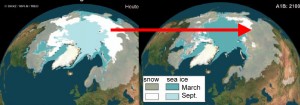
Die globale Erwärmung bewirkt ein Abschmelzen der polaren Eisgebiete am Nordpol. Hierdurch reduziert sich die Reflexion des Sonnenlichtes, ein Teil der Albedo A, und folglich ändert sich auch die Strahlungsbilanz unseres Planeten.
|
|