Download: Word     PDF

How does the climate equation work?

A simple model calculation

 The climate equation

We demonstrate the aerosol problem in a few simple calculations:

In a climate model there are certain factors which drive (force) the climate system. These forcings can be positive and lead to a warming. They can also be negative and lead to a cooling. We call a forcing “delta Q”. If the driving factors change with time (for example from industrialisation until today) because the greenhouse gases accumulate or the average solar radiation or cloudiness change, the average temperature on the Earth (“delta T”) also changes. The change in temperature is larger the more sensitive the climate system reacts to changes in the forcing. This climate sensitivity is expressed by the Greek letter “Lambda”.

We can write now:

Temperature change = climate sensitivity x forcing

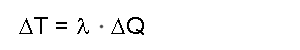with:

Temperature change in the considered time range

 What are the driving forces?

Climate research investigates which chemical and physical parameters stand behind these driving forces. A major factor are the greenhouse gases: carbon dioxide, methane, ozone, nitrous oxide, CFCs. Their fraction in the air has increased considerably since industrialisation. Greenhouse gases retain the energy of the infrared radiation close to the Earth. This radiative forcing brings in about +2.4 W/m².
There are some other forcings which can be either positive or negative but which have a less substantial impact. Finally aerosols play a major role, either by direct reflection of the sunlight or via formation of clouds. Our knowledge of the dimension of this effect is very poor. We can only guess that it may be in the range of –1 to –2 W/m².
 
We can now write a very simple equation about the sum of all driving factors:

 How strong is the impact of the aerosol cooling on the climate sensitivity?

A simple calculation with whole numbers demonstrates that the climate sensitivity is strongly dependent on the aerosol cooling. We assume that a temperature change of 2°C has been observed. Furthermore the climate forcing coming from greenhouse gases and other factors may sum up to 2 W/m². Since we do not know exactly what the contribution of the aerosol cooling is, we assume values of: 0 ;  -1 ;  -1.5 ; -1.75 W/m². What is the resulting climate sensitivity?

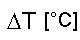
	forcing greenhouse gases + others	forcing aerosol
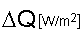
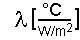
2	+ 2	0	2	1
2	+ 2	- 1	1	2
2	+ 2	- 1,5	0,5	4
2	+ 2	- 1,75	0,25	8

We see that the climate sensitivity takes values of 1, 2, 4 and 8°C per W/m². This is very uncertain. Such a wide uncertainty is also given in the scientific climate calculations. Climate models use, for example, sensitivities of 1.5 to 4.5°C per W/m².

The graph on the left shows the result with a grey shaded uncertainty range for a scientific calculation.

Graph: Climate sensitivity estimation based on the ‘Nature’ article of Andreae, Jones and Cox from 2005-06-30

 If the climate sensitivity is high ...

What will happen if we assume that the aerosol cooling is rather high (about 1.5 W/m²), but will decrease in the near future, while in parallel the amount of greenhouse gases in the air is increasing? We choose some numbers:

forcing greenhouse gases + others	forcing aerosol
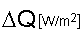
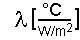
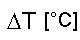
+ 2,5	1	1,5	4	6
+ 3	- 0,5	2,5	4	10

As we can see, the global temperature would increase significantly.

This example of a climate model calculation is strongly simplified. But it explains the basic thoughts which are behind the worries of the scientists.